1 RISC-V Introduction

1.1 Instruction Set Architecture (ISA)

Instruction Set Architecture (ISA) is the interface between software and hardware. And similar to the ISA, the assembly language is the intermediate language between the high-level language and the machine language.

Each CPU implements its own ISA, and the ISA is divided into two categories: CISC and RISC. CISC is the Complex Instruction Set Computer, and RISC is the Reduced Instruction Set Computer. The RISC-V is a RISC ISA, and it is an open-source ISA.

1.2 RISC-V Features

1.2.1 Registers

Since we use the RV32 variant of RISC-V, the registers are 32-bit wide. There are 32 registers in total, and they are named from x0 to x31.

Registers have no type. How to interpret the data in the registers is determined by the instructions that use them. Typically, we treat the content as a signed 32-bit integer.

2’s Complement Representation

Given an $n$-bit number, the value of the number is $-2^{n-1}\times b_{n-1}+{\sum }_{i=0}^{n-2}{2}^i\times b_i$, where $b_i$ is the $i$-th bit of the number.

More Info:

An easy way to convert a negative number to its 2’s complement representation is to first write the positive representation of the number, then flip all the bits, and finally add 1 to the result. Interestingly, we can convert a negative number (in 2’s complement representation) to its positive representation with the same steps.

1.2.2 Immediate Values

When a number is used as an immediate value, it is always first sign-extended to 32 bits. This means that the most significant bit of the number is copied to all the bits to the left of it.

1.2.3 Memory Layout

The memory layout of a RISC-V system is as follows:

Address	Content
Highest Address	Stack (grows downwards)
	Dynamic Data / Heap (grows upwards)
	Static Data (constants, etc.)
	Text (program code)
Lowest Address	Reserved

Note: Registers are not part of the memory layout.

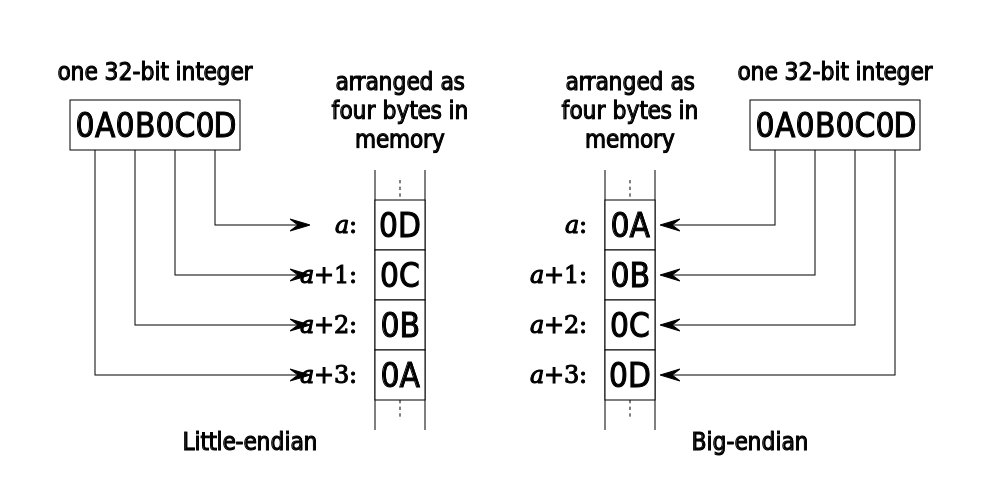
Endianness

RISC-V is a little-endian system. The endianness of a system determines the order in which the bytes of a multibyte number are stored in memory. There are two types of endianness: big-endian and little-endian. In a big-endian system, the most significant byte is stored at the lowest address, while in a little-endian system, the least significant byte is stored at the lowest address.

1.2.4 Logical Operations

There are two types of logical shifts: arithmetic shifts and logical shifts. In an arithmetic shift, the sign bit is copied to the left during a right shift, while in a logical shift, the sign bit is always 0.

Operation	Before	After
Logical Shift Right	1001	0100
Arithmetic Shift Right	1001	1100

2 RISC-V Procedure

2.1 Procedure Call

When a procedure is called, the following steps are taken:

Step	Implementation
Put parameters in a place where the callee can access them	Typically in registers a0 to a7
Transfer control to the callee	Using the jal instruction
Acquire the storage needed for the callee	Typically by decrementing the stack pointer
Perform the desired task
Place the result in a place where the caller can access it	Typically in register a0 - a1
Return control to the caller	Using the jalr instruction

2.2 Calling Convention

The registers in RISC-V are divided into two categories: caller-saved registers and callee-saved registers. The difference here is that if the callee modifies a callee-saved register, it must restore the original value before returning control to the caller. But for caller-saved registers, the callee can modify them freely.

In convention, callee should save the following registers: sp (stack pointer) and s0 to s11 (saved registers).

3 RISC-V Instruction Format

Type	Format	Feature
R-type	funct7 rs2 rs1 funct3 rd opcode	Take input from two registers and writes to one register
I-type	imm[11:0] rs1 funct3 rd opcode	Involves an immediate value, might be arithmetic or load operation
S-type	imm[11:5] rs2 rs1 funct3 imm[4:0] opcode	Store operation
B-type	imm[12] imm[10:5] rs2 rs1 funct3 imm[4:1] imm[11] opcode	Branch operation
U-type	imm[31:12] rd opcode	Load upper immediate
J-type	imm[20] imm[10:1] imm[11] imm[19:12] rd opcode	Jump operation

Note: The immediate value for B-type and J-type instructions needs to be left-shifted by 1 bit, while the immediate value for U-type instructions needs to be left-shifted by 12 bits.

More Info:

jalr instruction is usually used to return from a procedure call. But it can also be used to jump to a far away address. For example, to jump to any 32-bit address, we can use the following code:

    lui x1, <upper 20 bits>
    jalr x0, x1, <lower 12 bits>

If we want to jump to PC-relative address with 32-bit offset, we simply replace the lui instruction above with auipc instruction:

    auipc x1, <upper 20 bits>
    jalr x0, x1, <lower 12 bits>

4 Performance

4.1 Performance Metrics

There are two main performance metrics: response time and throughput. Response time is the time it takes to complete a task, while throughput is the number of tasks completed per unit time.

However, response time is not a good metric for performance evaluation because it includes all aspects of the system, such as the CPU, memory, and I/O devices. Instead, we usually use CPU time to evaluate the performance of a system, which is the time the CPU spends executing a task, excluding I/O time and other jobs’ share.

4.2 CPU Time

To calculate the CPU time, we use the following formula:

$$\text{CPU time}=\frac{\text{CPU clock cycles}}{\text{Clock rate}}=\frac{\text{Instruction Count}\times \text{CPI}}{\text{Clock rate}}$$

The performance depends on the following factors:

Component	IC	CPI	Clock Rate
Algorithm	Yes	Possible	No
Programming Language	Yes	Yes	No
Compiler	Yes	Yes	No
Instruction Set Architecture	Yes	Yes	Yes

5 Arithmetic

5.1 Addition and Subtraction

Addition overflows when the sum of two positive numbers is negative or the sum of two negative numbers is positive. Subtraction overflows when the difference of a positive number and a negative number is negative or the difference of a negative number and a positive number is positive.

Saturating Arithmetic

In saturating arithmetic, the result is set to the maximum or minimum value when an overflow occurs.

5.2 Multiplication

A primitive multiplier for $n$-bit numbers consists of a $2n$-bit ALU, a $2n$-bit register for the multiplicand, a $2n$-bit register for the product, and an $n$-bit register for the multiplier. The procedure is as follows:

1. Initialize the registers accordingly.

2. If the least significant bit of the multiplier is 1, add the multiplicand to the product.

3. Shift the product left by 1 bit.

4. Shift the multiplier right by 1 bit.

5. Repeat steps 2 to 4 for $n$ iterations.

6. The product register contains the result.

Here is an example of multiplying 2 by 7:

Iteration	Multiplier	Multiplicand	Product	Operation
0	0111	0000_0010	0000_0000	Initialization
1	0111	0000_0010	0000_0010	Add multiplicand
	0011	0000_0100	0000_0010	Shift registers
2	0011	0000_0100	0000_0110	Add multiplicand
	0001	0000_1000	0000_0110	Shift registers
3	0001	0000_1000	0000_1110	Add multiplicand
	0000	0001_0000	0000_1110	Shift registers
4	0000	0010_0000	0000_1110	Shift registers

An optimized multiplier for $n$-bit numbers consists of an $n$-bit ALU, an $n$-bit register for the multiplicand, and a $2n$-bit register for the product. The procedure is as follows:

1. Initialize the multiplicand register with the multiplier. Initialize the product register’s lower $n$ bits with multiplier and the upper $n$ bits with 0.

2. If the least significant bit of the product register is 1, add the multiplicand to upper $n$ bits of the product register.

3. Shift the product register right by 1 bit.

4. Repeat steps 2 and 3 for $n$ iterations.

5. The product register contains the result.

Here is an example of multiplying 2 by 7:

Iteration	Multiplicand	Product	Operation
0	0010	0000_0111	Initialization
1	0010	0010_0111	Add multiplicand
	0010	0001_0011	Shift right
2	0010	0011_0011	Add multiplicand
	0010	0001_1001	Shift right
3	0010	0011_1001	Add multiplicand
	0010	0001_1100	Shift right
4	0010	0000_1110	Shift right

5.3 Division

A primitive divider for $n$-bit numbers consists of a $2n$-bit ALU, a $2n$-bit register for the divisor, a $2n$-bit register for the remainder, and an $n$-bit register for the quotient. The procedure is as follows:

1. Initialize the divisor register’s upper $n$ bits with the divisor and the lower $n$ bits with 0. Initialize the remainder register’s lower $n$ bits with the dividend and the upper $n$ bits with 0. Initialize the quotient register with 0.

2. Subtract the divisor from the remainder.

3. If the result is negative, add the divisor back to the remainder. Shift the quotient left by 1 bit and add 0 to the least significant bit. Else, shift the quotient left by 1 bit and add 1 to the least significant bit.

4. Shift the divisor right by 1 bit.

5. Repeat steps 2 to 4 for $n+1$ iterations.

6. The quotient register contains the quotient, and the remainder register contains the remainder.

Here is an example of dividing 7 by 2:

Iteration	Divisor	Remainder	Quotient	Operation
0	0010_0000	0000_0111	0000	Initialization
1	0010_0000	1110_0111	0000	Subtract divisor
	0010_0000	0000_0111	0000	Restore
	0001_0000	0000_0000	0000	Shift registers
2	0001_0000	1111_0111	0000	Subtract divisor
	0001_0000	0000_0111	0000	Restore
	0000_1000	0000_0000	0000	Shift registers
3	0000_1000	1111_1111	0000	Subtract divisor
	0000_1000	0000_0111	0000	Restore
	0000_0100	0000_0000	0000	Shift registers
4	0000_0100	0000_0011	0000	Subtract divisor
	0000_0010	0000_0011	0000	Shift registers
	0000_0010	0000_0011	0001	Add 1 to quotient
5	0000_0010	0000_0001	0001	Subtract divisor
	0000_0001	0000_0001	0010	Shift registers
	0000_0001	0000_0001	0011	Add 1 to quotient

An optimized divider for $n$-bit numbers consists of an $n$-bit ALU, an $n$-bit register for the divisor, and a $2n$-bit register for the remainder. The procedure is as follows:

1. Initialize the divisor register with the divisor. Initialize the lower $n$ bits of the remainder register with the dividend and the upper $n$ bits with 0.

2. Shift the remainder register left by 1 bit.

3. Subtract the upper $n$ bits of the remainder register from the divisor.

4. If the result is negative, add the divisor back to the upper $n$ bits of the remainder register, else add 1 to the lower $n$ bits of the remainder register.

5. Repeat steps 2 to 4 for $n$ iterations.

6. The lower $n$ bits of the remainder register contain the quotient, and the upper $n$ bits contain the remainder.

Here is an example of dividing 7 by 2:

Iteration	Divisor	Remainder	Operation
0	0010	0000_0111	Initialization
1	0010	0000_1110	Shift left
	0010	1110_1110	Subtract divisor
	0010	0000_1110	Restore
2	0010	0001_1100	Shift left
	0010	1111_1100	Subtract divisor
	0010	0001_1100	Restore
3	0010	0011_1000	Shift left
	0010	0001_1000	Subtract divisor
	0010	0001_1001	Add 1
4	0010	0011_0010	Shift left
	0010	0001_0010	Subtract divisor
	0010	0001_0011	Add 1

Sign Convention

In signed division, the sign of the quotient is negative if and only if the signs of the dividend and divisor are different. The remainder has the same sign as the dividend. For example, $-7÷2=-3\mathrm{\cdots }-1$.

6 Floating Point Arithmetic

6.1 Floating Point Representation

A floating point number consists of three parts: the sign bit, the exponent, and the fraction (mantissa). The value of the number is:

$${(-1)}^s\times 2^{e-B}\times 1.f$$

where $s$ is the sign bit, $e$ is the exponent, $B$ is the bias, and $f$ is the fraction.

Bias

The bias is calculated as $2^{k-1}-1$, where $k$ is the number of bits used to represent the exponent. The purpose of the bias is to treat the exponent as an unsigned number.

Relative Precision

The relative precision is $2^{-f}$, where $f$ is the number of bits used to represent the fraction. To convert the relative precision to the number of decimal places, we use the formula $-{\log }_{10}(2^{-f})=f\times {\log }_{10}2$.

6.2 Floating Point Special Encoding

There are three special encodings for floating point numbers: zero, infinity, and NaN (Not a Number). Zero is represented by all bits being 0, infinity is represented by the exponent being all 1s and the fraction being 0, and NaN is represented by the exponent being all 1s and the fraction being non-zero. To be noticed, there are two types of infinity: positive and negative (determined by the sign bit).

There is also a denormalized representation for floating point numbers. In this representation, the exponent is 0, and the fraction is non-zero. The value of the number is:

$${(-1)}^s\times 2^{1-B}\times 0.f$$

The overall representation of floating point numbers is as follows:

Exponent	Fraction = 0	Fraction $\mathrm{\ne }$ 0
0	$\pm 0$	Denormalized
1 to $2^k-2$	Normalized	Normalized
$2^k-1$	$\pm \mathrm{\infty }$	NaN

Easy to Mistake:

When calculating the range of a normalized floating point number, we need to be careful with the exponent. The minimum exponent is 1, and the maximum exponent is $2^k-2$. 0 and $2^k-1$ are reserved for special encodings.

6.3 Floating Point Arithmetic

The procedure for floating point addition and subtraction is as follows:

1. Align the exponents of the two numbers, the final exponent is the larger of the two exponents.

2. Add or subtract the significands of the two numbers.

3. Normalize the result (shift the significand until ).

4. Round the result (and renormalize if necessary).

The procedure for floating point multiplication is as follows:

1. Add the exponents of the two numbers.

2. Multiply the significands of the two numbers.

3. Normalize the result (shift the significand until ).

4. Round the result (and renormalize if necessary).

5. Determine the sign of the result.

7 Pipeline

7.1 Inefficiency of Single Cycle CPU

In a single cycle CPU, the clock cycle is determined by the slowest instruction (the longest delay). This means most module will be idle for most of the time, which is inefficient.

7.2 Pipeline Performance

Suppose all stages are balanced, the speedup of a pipeline is given by:

$${\text{Clock Cycle Time}}_{\text{pipelined}}=\frac{{\text{Clock Cycle Time}}_{\text{non-pipelined}}}{\text{Number of Stages}}$$

To be noticed that the latency (time to complete a single instruction) of a pipelined CPU will not be reduced. In fact, the latency may increase especially when stages are not balanced. Pipeline is more about throughput (number of instructions completed per unit time) than latency.

7.3 Pipeline Hazards

There are three types of pipeline hazards: structural hazards, data hazards, and control hazards.

• Structural hazards: Two instructions require the same hardware resource.

• Data hazards: The next instruction to execute requires the result of the current instruction.

• Control hazards: Which instruction to execute next is determined by the result of the current instruction.

The structure hazards do not occur in RISC-V, because the ISA is designed under Harvard architecture (separate instruction and data memory). This avoids the conflict between instruction fetch and data access. The two other hazards, however, still exist.

7.3.1 Data Hazards

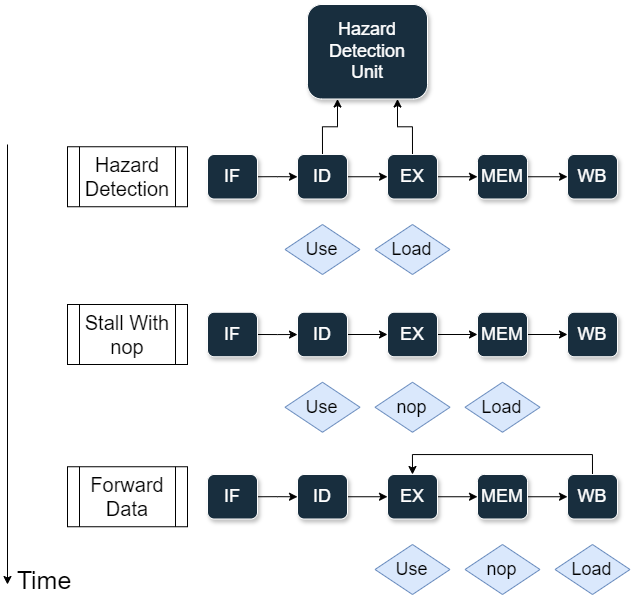
Generally, we solve data hazards by either stalling the pipeline or forwarding the data, sometimes a combination of both.

Stall Only

When stalling the pipeline, we insert a no-operation (NOP) instruction to the pipeline. This is the simplest way to solve data hazards, but it is also the least efficient.

Forwarding Only

We add extra data path to forward the data from the output of the ALU (or memory) to the input of the ALU. Forwarding data from ALU to ALU is called EX-EX forwarding (or ALU-ALU forwarding), while forwarding data from memory to ALU is called MEM-EX forwarding (or MEM-ALU forwarding). However, this method is not always applicable (cannot handle load-use hazards).

Stall and Forwarding

We stall the pipeline only when forwarding is not possible (load-use hazards), which requires more modules for hazard detection and control.

Figure 1: Stall and Forwarding for Load-Use Hazards

7.3.2 Control Hazards

Generally, we solve control hazards by stalling and flushing the pipeline. When a branch instruction is detected, we stall the pipeline (by inserting NOPs or filling the pipeline with predicted instructions). After we know the result of the branch instruction, we can check if the prediction is correct. If it is not, we flush the pipeline (discard the instructions after the branch instruction) and restart the pipeline.

If extra hardware is available, we can determine the branch target early in the instruction decode stage and reduce the number of stalls.

Static and Dynamic Branch Prediction

In static branch prediction, the prediction is made at compile time by the compiler. In dynamic branch prediction, the prediction is made at run time by looking at the history of the branch instruction.

8 Instruction-Level Parallelism

8.1 Deeper Pipeline

If we further break down the process and hence have more stages in the pipeline, we can achieve shorter clock cycle time (please refer to Section 7.2).

8.2 Multiple Issue

Multiple issue means execute multiple instructions in parallel in a single clock cycle (This may cause CPI to be less than 1. If so we use IPC, Instructions Per Cycle). The key procedure of multiple issue is to resolve instruction dependencies and pack instructions into issue packets.

8.2.1 Static Multiple Issue

In static multiple issue, compilers is responsible for reordering the instructions to avoid hazards. This is also called Very Long Instruction Word (VLIW) architecture.

Data Dependencies

It is obvious that two instructions that one depends on the other cannot be issued in parallel. For example, a load instruction that requires the address calculated by the previous instruction.

Hardware Race

The critical problem for hardware is that the data memory can only be accessed once in a clock cycle. Hence, two instructions that both require data memory access cannot be issued in parallel. This is why the issue packet is designed to have one slot for ALU / Branch instruction (which does not require data memory access) and one slot for Load / Store instruction (which requires data memory access).

Example:

For this loop assembly code:

lw	t0, 0(s1)	s1 is pointer to the array
add	t0, t0, s2	add a constant to the arrayelement
sw	t0, 0(s1)	store the result back to the array
addi	s1, s1, -4	move to the next element
bge	s1, zero, loop	loop back

The optimal reordering for an 2-issue processor will have an IPC of 1.25:

ALU / Branch	Load / Store
nop	lw t0, 0(s1)
addi s1, s1, -4	nop
add t0, t0, s2	nop
bge s1, zero, loop	sw t0, 0(s1)

To be noticed that the add and addiinstructions cannot be swaped, otherwise it will cause a load-use hazard.

Loop Unrolling

One technique to resolve name dependencies is Loop Unrolling. For example, if we have a loop that loads an element from an array, perform some operations, and store the result back to the array, and the loop is executed for 4 times. This loop cannot be issued in parallel because the loop body use the same register and every instruction depends on this register. This is so-called name dependencies, because the dependencies is not caused by data but reusing register name. To resolve this, we can unroll the loop, which means we copy the loop body 4 times and change the register name for each copy. This way, the instructions in different loop bodies can be issued in parallel.

    // Original Loop
    for (int i = 0; i < 4; i++) {
        A[i] = A[i] + 1; // use the same register to hold A[i]
    }

    // Unrolled Loop
    A[0] = A[0] + 1; // use different register for A[0], A[1], A[2], A[3]
    A[1] = A[1] + 1;
    A[2] = A[2] + 1;
    A[3] = A[3] + 1;

8.2.2 Dynamic Multiple Issue

In dynamic multiple issue, the CPU examines the instruction stream and decides which instructions to execute in parallel. This is also called “Superscalar” architecture.

Out-of-Order Execution

In out-of-order execution, the CPU executes the instructions in the order that minimizes the pipeline stalls. It Involves three steps: in-order issue: issue the instructions to the reservation station in order; out-of-order execution: execute the instructions in the reservation station whenever the operands are ready; in-order commit: commit the instructions in order to the register file.

8.3 Speculative Execution

In speculative execution, the CPU executes the instructions before it knows whether they should be executed. This is used to reduce the branch penalty. Additionally, this helps load cache data before it is needed.

8.4 Register Renaming

Register renaming is used to resolve the name dependencies. The CPU uses a physical register file to store the data, and a mapping table to map the logical register to the physical register. This way, the CPU can issue the instructions in parallel even if they use the same logical register.

9 Memory Hierarchy

9.1 Cache

9.1.1 Direct Mapped Cache

In a direct mapped cache, each memory block can only be stored in one specific cache block. The cache block is determined by the lower bits of the memory block address. The cache block consists of the tag, the index, the valid bit, and the data, and the number of bits in each part is calculated as follows:

$\mathrm{\#}\text{Offset bits}$$={\log }_2(\text{Block Size})$

$\mathrm{\#}\text{Index bits}$$={\log }_2(\text{Number of Blocks})$

$\mathrm{\#}\text{Tag bits}$$=\text{Address bits}-\text{Offset bits}-\text{Index bits}$

Easy to Mistake:

For fixed-sized cache, increasing the block size may not necessarily reduce the miss rate. This is because the larger block size will decrease the number of blocks in the cache, which may lead to more conflicts. Also, the larger block size will increase the miss penalty (the time to load a block from memory to cache).

9.1.2 Set Associative Cache

In a set associative cache, several cache blocks are mapped to the same set. Each memory block can only be stored in one of the cache set but can be stored in any block within the set. The cache block consists of the tag, the index (set), the valid bit, and the data, and the number of bits in each part is calculated as follows:

$\mathrm{\#}\text{Offset bits}$$={\log }_2(\text{Block Size})$

$\mathrm{\#}\text{Index bits}$$={\log }_2(\text{Number of Sets})$

$\mathrm{\#}\text{Tag bits}$$=\text{Address bits}-\text{Offset bits}-\text{Index bits}$

9.1.3 Fully Associative Cache

In a fully associative cache, each memory block can be stored in any cache block. The cache block consists of the tag, the valid bit, and the data, and the number of bits in each part is calculated as follows:

$\mathrm{\#}\text{Offset bits}$$={\log }_2(\text{Block Size})$

$\mathrm{\#}\text{Tag bits}$$=\text{Address bits}-\text{Offset bits}$

9.1.4 Multi-Level Cache

In a multi-level cache, we put the L1 cache (smaller but faster) closer to the CPU and the L2 cache (larger but slower) further away. This layout effectively reduces the miss rate.

More Info:

The overall storage system can be viewed as a huge multi-level cache, consisting of the CPU registers, the L1 cache, the L2 cache, the main memory, and the disk. The closer the storage is to the CPU, the faster but smaller it is.

9.1.5 Pros and Cons of Different Cache

Generally, the higher the associativity, the lower the miss rate. However, to achieve higher associativity, we need more hardware (comparators, etc.), which increases the cost of the cache and the access time.

9.2 Cache Miss

There are three types of cache miss: compulsory miss, capacity miss, and conflict miss.

• Compulsory miss: On startup, the cache is empty, so the first access to a memory block will always miss.

• Capacity miss: The cache is full. Hence, any new memory block must replace an existing block.

• Conflict miss: Although the cache is not full, the memory block cannot be stored in the cache because of the block (or set) it maps to is already occupied (only for set associative or direct mapped cache).

We can optimize the cache design to reduce the miss rate. Below are some common trade-offs:

Trade-off	Pros	Cons
Increase cache size	Reduce capacity miss	Higher access time
Increase associativity	Reduce conflict miss	Higher access time and extra hardware
Increase block size	Reduce compulsory miss	Higher miss penalty

9.3 Write Policy

On write hit (the memory block we want to write is already in the cache), we can use write-through or write-back policy.

• Write-through: The data is written to both the cache and the memory. This is simpler but slower.

• Write-back: The data is written to the cache only. The data in the memory is updated only when the cache block is replaced. This is faster but more complex and require an extra dirty bit (to indicate whether the cache block is modified) for each cache block.

On write miss (the memory block we want to write is not in the cache), we can use write-allocate or write-around policy.

• Write-allocate: The memory block is loaded into the cache and then the data is written to the cache.

• Write-around: The data is written to the memory only. The cache is not updated.

9.4 Cache Performance

The cache performance is evaluated by Average Memory Access Time (AMAT), which is calculated as follows:

$$\text{AMAT}=\text{Hit Time}+\text{Miss Rate}\times \text{Miss Penalty}$$

For multi-level cache, the miss rate is divided into each level, and sometimes calculated within the level (local miss rate) or globally (global miss rate). The difference is shown as follows:

${\text{Global Miss Rate for level}}_i$$={\displaystyle \frac{{\text{Total number of misses on level}}_i}{\text{Total number of block requests}}}$

${\text{Local Miss Rate for level}}_i$$={\displaystyle \frac{{\text{Number of misses on level}}_i}{{\text{Number of block requests on level}}_i}}$

The AMAT for multi-level cache is calculated by using the global miss rate:

AMAT$=\text{L1 Hit Time}$

$+\text{L1 Global Miss Rate}\times \text{L1 Miss Penalty}$

$+\text{L2 Global Miss Rate}\times \text{L2 Miss Penalty}$

or by using the local miss rate:

AMAT$=\text{L1 Hit Time}$

$+\text{L1 Local Miss Rate}$

$\times \left(\text{L1 Miss Penalty}+\text{L2 Local Miss Rate}\times \text{L2 Miss Penalty}\right)$

9.5 Dependability Measures

There are three metrics to evaluate the dependability of a cache: mean time to failure (MTTF), mean time to repair (MTTR), and availability. The availability is calculated as follows:

$$\text{Availability}=\frac{\text{MTTF}}{\text{MTTF}+\text{MTTR}}$$

9.6 Error Detection and Correction

9.6.1 Hamming Distance

The Hamming distance is the minimum number of bit flips required to convert one valid pattern to another.

For Hamming distance $d=2$, this allows single-bit error detection. For Hamming distance $d=3$, this allows single-bit error correction. The difference is caused by some points that are equidistant to two valid patterns.

9.6.2 Hamming Code

In this course, we only consider SEC / DED codes (Single Error Correction / Double Error Detection), where Hamming Code is the most common example. The Hamming Code is constructed as follows:

1. Determine the number of parity bits required by the formula $2^p\ge m+p+1$, where $m$ is the number of data bits and $p$ is the number of parity bits.

2. The positions of the parity bits are determined by the power of 2 (1, 2, 4, 8, etc.), and each parity bit is named by its position ($p_1,p_2,p_4,p_8,\mathrm{\dots }$).

3. Let the parity bit $p_{2^i}$ checks the parity of the bits where the $i$-th bit is 1 (including itself). The overall parity should be even.

To detect and correct errors, we can use the following steps:

1. Calculate the parity bits using the data bits.

2. Compare the calculated parity bits with the received parity bits.

3. If the parity bits are different, there is an error. The position of the error is determined by the sum of subscript of the parity bits that are different. For example, if $p_1$ and $p_4$ are different, the error is at the 5-th bit.

Double Error Detection

To detect double errors, we can add an extra parity bit $p_n$ that checks the parity of all bits. If there is only one error, $p_n$ will be incorrect. If there are two errors, $p_n$ will still be correct, but some other parity bits will be incorrect.

9.7 Virtual Memory

9.7.1 Page Table

Sometimes we increase the address space by using virtual memory, with some parts stored in the disk. Hence, before accessing the memory, we need to translate the virtual address to the physical address. The translation is done with the help of the page table.

The page table contains all mappings from virtual pages to physical pages. Hence, there is no index bit in the page table, because the virtual page number is the index. The page table consists of the valid bit and the physical page number.

9.7.2 Translation Look-aside Buffer (TLB)

Since page table needs to hold all mappings, it is large and can only be stored in the main memory. However, main memory access is slow. To speed up the translation, we use TLB, which is a small cache for the page table.

Since the TLB is essentially a cache, the structure is the same as the previous section mentioned, and we will not repeat it here.

9.8 Overall Memory Hierarchy

When fetching data, we go through the following steps:

1. Translate the virtual address to the physical address.

   1. Check TLB. If the translation is in the TLB, use the physical page number directly. Else, go to the next step.

   2. Access the page table in the main memory. If the physical page number is located on disk, raise a page fault. Else, use the physical page number.

2. Access the cache. If the data is in the cache, use the data directly. Else, go to the next step.

3. Access the main memory.

Easy to Mistake:

There are two scenarios that will never happen:

1. We miss both the TLB and page table but hit the cache (or memory): Unless a page fault occurs, the data must be in the cache or memory.

2. We hit TLB but miss the page table: Since the TLB is a cache for the page table, and page table is the only source for the physical page number.

Note: TLB miss here means the page we required is not in memory, not we cannot find the virtual page number in TLB (which is impossible).

10 Parallel Processor

The goal of parallel processor is to replace large inefficient processors with multiple smaller processors, which improves scalability, availability and power efficiency.

Parallelism can be achieved in multiple ways:

• Task-level parallelism: execute independent jobs in parallel.

• Parallel processing program: One program that utilize multiple processors.

• Multicore processor: Multiple processors on a single chip.

However, the challenge of parallelism comes from both hardware and software. The hardware challenge is that serial hardware is much simpler than parallel hardware. The software challenge is sequential program is much easier to write and debug than concurrent program.

10.1 Amdahl’s Law

Amdahl’s Law is used to evaluate the speedup of a program when parallelized. The speedup is calculated as follows:

$$\text{Speedup}=\frac{1}{(1-f)+\frac{f}{n}}$$

where $f$ is the fraction of the program that can be parallelized and $n$ is the number of processors.

The maximum speedup is given by:

$$\underset{n\to \mathrm{\infty }}{lim}\text{Speedup}=\frac{1}{1-f}$$

Amdahl’s law tells us we can never achieve reverse proportional speedup by adding more processors, due to the presence of the serial part of the program, as the maximum speedup is $\frac{1}{1-f}$.

More Info:

How Amdahl’s Law is derived:

Speedup$={\displaystyle \frac{T_{\text{old}}}{T_{\text{new}}}}$

$={\displaystyle \frac{T_{\text{old}}}{(1-f)\times T_{\text{old}}+\frac{f\times T_{\text{old}}}{n}}}$

$={\displaystyle \frac{1}{(1-f)+\frac{f}{n}}}$

Strong and Weak Scalability

Strong scalability is that if the problem size is fixed, the time should be reversed proportional to the number of processors. Weak scalability is that if the number of processors is proportional to the problem size, the time should be constant. Weak scalability is more common in practice and strong scalability is more difficult to achieve, due to Amdahl’s Law.

10.2 Single Instruction Multiple Data (SIMD)

In SIMD, processor operates on a vector of data with a single instruction. Or, all processors execute the same instruction, but each with different data address. This is a simple way to achieve synchronization.

10.3 Multithreading

In multithreading, processor can switch between different threads to achieve parallelism. When one thread is stalled, the processor can switch to another thread. There are two types of multithreading: fine-grained multithreading (switch between threads in every cycle) and coarse-grained multithreading(switch only on long stalls, such as cache miss).

Simultaneous Multithreading (SMT)

In SMT, the processor can execute multiple threads simultaneously. This is achieved by multiple-issue processor. SMT utilize resources more efficiently than the two types of multithreading mentioned above. In traditional multithreading, only one thread can use the resources at a time. This usually cannot fully utilize all issue slots in the processor. In SMT, the vacant resources can be used by another thread.

10.4 Shared Memory Multiprocessor

In shared memory multiprocessor, all processors share the same memory. Hence, if one program is written into the memory, all processors can read it.

10.5 Message Parsing Multiprocessor

In message parsing multiprocessor, each processor has its own memory. The processors communicate with each other by sending messages. This is more scalable than shared memory multiprocessor, but the communication is more complex.